How To Compute Arbitrary Precision Transcendental Numbers
Rodrigo Montegasppα Cacilhας
13 Apr 2021
•
5 min read
Transcendental numbers are probably the most useful tools in Mathematics. They are irrational numbers that cannot be expressed using a finite formula.
For example, the Euler’s identity is considered the most beautiful Mathematical formula (perhaps I’m gonna explore it in the future):
It exposes a relation between the two most important transcendental numbers, the complex numbers, the unit and the null / zero. It’s used mostly in rotation over real 𝑣𝑠 imaginary axes, on complex exponential, roots, and other useful operations.
Yet, it’s useless if one doesn’t know how to get 𝑒 and π in the required precision.
Euler’s constant
The Euler’s constant or Euler’s number, 𝑒 for short, is the ratio describing any constant growth. It’s defined as:
![𝑒 = lim_(n→+∞)[1+(1/n)]^n](https://cacilhas.info/img/euler.png)
It’s about 2.71828…. 𝑒 is kinda magical number, poping up in a lot of Mathematical problems, offering good and easy solutions, since complex number operations to logarithm, exponential, and other kinds of growth behaviour.
But how to get to the desired precision?
One can take this formula and compute greater and greater 𝑛 values, until it reaches the required precision. Nevertheless, the exponent can be quite intimidating, leading to an undesired weak performance – similar or worst than the π computation below. Yet, it’s hard to say how long it must go to getta the desired precision.
Fortunately another Euler’s formula gives us a better solution:
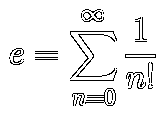
This formula is very convenient, ’cause it increases the precision every step in an easly predictable way:
- 1/0! = 1/1 = 1
- 1 + 1/1! = 1 + 1/1 = 2
- 2 + 1/2! = 2 + 1/2 = 2.5
- 2.5 + 1/3! = 2.5 + 1/6 ≈ 2.6667
- 2.6667 + 1/4! ≈ 2.6666 + 1/24 ≈ 2.7083
- 2.7083 + 1/5! ≈ 2.7083 + 1/120 ≈ 2.7167
- 2.7167 + 1/6! ≈ 2.7177 + 1/720 ≈ 2.7180
- ⋱
- prev. + 1/∞! = 𝑒
It’s easly predictable ’cause the precision equals to log₁₀(n!):
- n = 0 → log₁₀(0!) = log₁₀(1) = 0
- n = 1 → log₁₀(1!) = log₁₀(1) = 0
- n = 2 → log₁₀(2!) = log₁₀(2) ≈ 0.3010
- n = 3 → log₁₀(3!) = log₁₀(6) ≈ 0.7782
- n = 4 → log₁₀(4!) = log₁₀(24) ≈ 1.3802
- n = 5 → log₁₀(5!) = log₁₀(120) ≈ 2.0792
- ⋱
- n = 1000 → log₁₀(1000!) ≈ 2567.60461
It gets big very quickly.
More everyday case
Image one needs to calculate 𝑒 to the 80-bit precision. That doesn’t differ from before. Bits are binary digits, i.e, 2-base numbers. So, instead of log₁₀, one must use log₂:
- log₂(n!) ≈ 80
- 2log₂(n!) ≈ 280
- n! ≈ 2⁸⁰
- 25! < 2⁸⁰ < 26!
So, 26 steps are good enough.
Let’s implement it using Python:
from numbers import Integral, Rational
from typing import Callable
# Lazy factorial implementation
fact: Callable[[Integral], Integral] = lambda n: prod(range(1, n+1))
# An LRU cached version, if you prefer:
#
# from functools import lru_cache
#
# fact: Callable[[Integral], Integral] = lambda n: lru_cache(
# 1 if n <= 0 else (n * fact(n - 1))
# )
def steps(prec: Integral) -> Integral:
res = 1
while fact(res) >> prec == 0:
res += 1
return res
The right shift (>>) returns zero as long as the value‘s less bit wide than
the precision.
Now let’s compute 𝑒 itself:
compute_e: Callable[[Integral], Rational] = lambda prec: sum(
1./fact(x) for x in range(prec)
)
The solutions coming out from it is:
>>> calculate_e(steps(64)) # Python uses 64-bit floats
2.7182818284590455
>>> math.e
2.718281828459045
Not bad at all. In fact, we reach the 64-bit precision with only 18 iterations.
Performance
We’re not worried about performance here, it’s not this post’s scope. We’re just showing how it works and how you can implement and use it.
What about π?
π is the ratio of any circle’s perimeter (circumference) to its diameter. That’s π very definition.
However, it’s a transcendental number and needs an infinity serie to be computed. Leibniz gave us a neat solution:
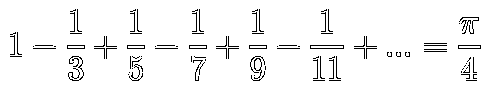
The process is quite the same used for 𝑒, take the formula:
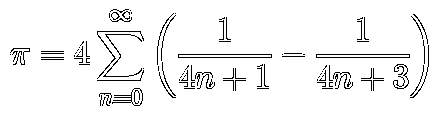
Then get the precision:
compute_pi: Callable[[Integral], Rational] = lambda prec: 4. * sum(
(1./(4*n+1) - 1./(4*n+3)) for n in range(prec)
)
Tip: the precision is log₂(4n), so n = 2prec-2, which one can get by left shifting. Note that we got exactly the inverse of the previous calculation: here the necessary steps amount grows very fast with small gain.
So you may get disappointed when running:
>>> compute_pi(1 << (64 - 2))
This computation is way more inefficient than the previous one – Python isn’t that good in dealing with floating-point operation and it’s necessary a humongous amount of steps to getta the target. I recomend 5M steps:
>>> compute_pi(5000000)
3.141592553588895
>>> math.pi
3.141592653589793
To this task, one’s gonna need a tougher tool, as C and multithreading. Again performance is not this post’s scope. Probably it requires using some C cast spells in order to optimise the computation.
Or you can go down through the Wolfram MathWorld’s or Wolfram Alpha’s π page references in search of better formulæ. I did it, and I can ensure they are, including serie representations.
WorksHub
Jobs
Locations
Articles
Ground Floor, Verse Building, 18 Brunswick Place, London, N1 6DZ
108 E 16th Street, New York, NY 10003
Subscribe to our newsletter
Join over 111,000 others and get access to exclusive content, job opportunities and more!
